Кроме качественного, имеется и количественное согласие. Длина волны де Бройля k=h/MV, где M ЂЂЂ масса частицы, V ЂЂЂ её скорость, h ЂЂЂ постоянная Планка. Чем выше скорость и энергия электрона, тем короче отвечающая ему длина волны. Судя по положению дифракционных максимумов, с ростом энергии электрона длина волны именно так и убывает. То же даёт и классическая картина явления. На кристалле дифрагируют не электроны, а вызванные ими рентгеновские лучи, длина волны k которых по законам фотоэффекта связана с энергией электрона E=hf=hc/k, или k=hc/E. То есть и в классике длина волны дифрагирующего излучения падает с ростом энергии электронов. Поскольку в опытах исследуют быстрые электроны со скоростями порядка скорости света c, их импульс p=MV выражают через энергию формулой E=pc=MVc. Отсюда найдём k=hc/E=h/MV, что совпадает с формулой де Бройля.
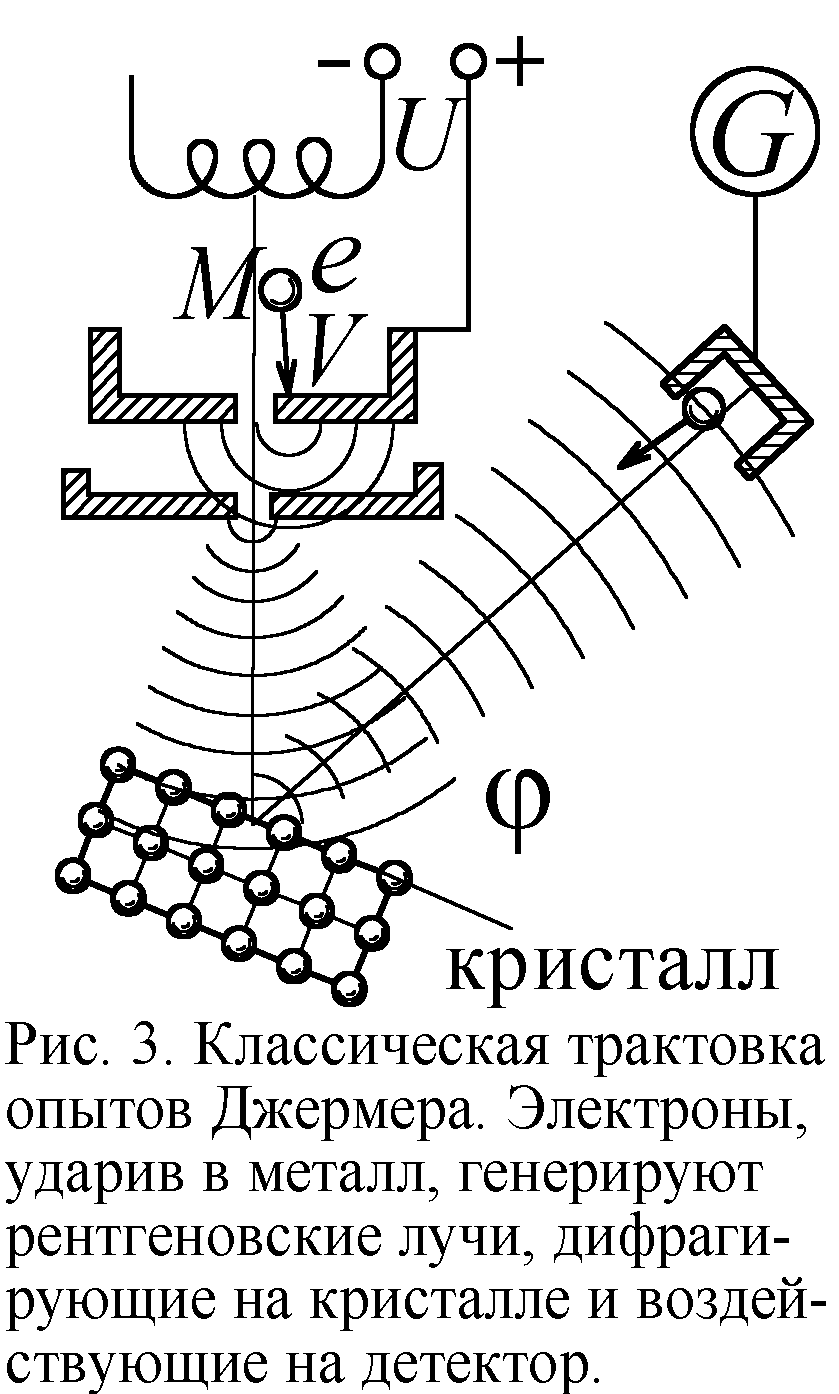
Если же в качестве детектора использован гальванометр, меряющий величину тока, заряда, приносимого электронами, то и его показания могут быть вызваны рентгеновскими лучами. Лучи могут наводить ток, фото-эдс в гальванометре, а могут выбивать электроны из детектора, рождая ток, обратный тому, что дают электроны. Поэтому кроме величины тока гальванометра, надо измерять его знак ЂЂЂ соответствует ли он привнесению электронов или их уходу? Величина фототока, как гласит закон Столетова, пропорциональна интенсивности излучения. Поэтому там, где дифракция рентгеновских лучей даёт максимумы, будет максимален и фототок, что интерпретируют как рост числа падающих электронов, а где минимумы, там фототок мал, и считают, что в эти области электроны почти не попадают (рис. 3).
Однако физики не учли, что электроны при ударе о металл всегда генерируют электромагнитные волны. И наоборот, электромагнитные волны, свет, попав в металл, вырывают из него электроны (фотоэффект, рис. 2). Поэтому не исключено, что реально на кристалле никеля дифрагируют не сами электроны, а созданное ими ещё в электронной пушке электромагнитное рентгеновское излучение. Не зря сравнивают дифракцию на кристалле электронов и рентгеновских лучей. И детектор, призванный регистрировать электроны, обнаруживает именно рентгеновские лучи. Ведь фотоплёнку, часто применяемую для регистрации дифракционной картины, способны засвечивать как электронные пучки, так и рентгеновские лучи.
Первым опытом, "подтвердившим" волновую природу электрона, был опыт Дэвисона и Джермера, которые облучали кристалл никеля высокоэнергичными электронами [ ]. Те рассеивались поверхностью кристалла неравномерно: в некоторых направлениях электронов вылетало больше, в других ЂЂЂ меньше. Максимумы и минимумы рассеяния чередовались как при дифракции света на дифракционной решётке или рентгеновских лучей на кристалле (рис. 1). Поэтому сочли, что электроны подобны волне, рассеиваемой поверхностью кристалла, атомы которого играют ту же роль, что штрихи отражательной дифракционной решётки. Казалось, это подтверждали и численные оценки длин волн электронов по их энергиям.
Пожалуй, нет более странного утверждения квантовой механики, чем гипотеза де Бройля, по которой всякую частицу надо одновременно рассматривать как волну, а волну ЂЂЂ как частицу. Но учёные приняли сей парадоксальный тезис, нарушающий столь почитаемый ими принцип Оккама, по которому свет незачем рассматривать как частицу, раз можно объяснить его свойства, считая свет волной, и не стоит считать электроны и атомы волнами, раз легко понять их свойства как частиц. Впрочем, казалось, электроны в опытах проявляли и волновую природу, а свет ЂЂЂ корпускулярную. Но, как было показано [ ], эти опыты можно объяснить и классически ЂЂЂ считая электрон просто частицей, а свет ЂЂЂ простой волной. Эти объяснения не были найдены потому, что физики, ослеплённые успехами квантовой механики, и не пытались их найти. Так есть ли доказательства корпускулярно-волнового дуализма?
Не следует без необходимости умножать сущности
БРИТВА ОККАМА и ДИЛЕММА: ЧАСТИЦА ИЛИ ВОЛНА?(напечатано в журнале " " ЂЂЂ6, 2008)
Семиков С.А. "Бритва Оккама и дилемма: частица или волна?"
Комментариев нет:
Отправить комментарий